Dolt is the first version controlled SQL database, built on Prolly Trees. Prolly Trees are the novel data structure that power's Dolt's unique storage layer, making it possible to manage multiple branches in a space-efficient way. Here at Dolthub, we're kind of obsessed with them.

We didn't invent them: noms gets credit for that. But we saw their potential as a building block for decentralized applications. And we're not the only ones noticing: BlueSky has their own implementation that they call Merkle Search Trees.

Originally we just used Prolly Trees for our table indexes. But since then, we've found more and more uses for them, like indexable JSON that doesn't sacrifice deserialization speed..

Now we're turning our heads to vector databases. To the best of our knowledge, no SQL database on the market supports branching and merging vector data. We know this because Dolt is the only SQL database to have true support for branches, and Dolt doesn't have vector support... yet.

SQL databases provide vector support in the form of Vector Indexes, indexes optimized for vector similarity search. A vector index built on top of Prolly Trees would unlock lots of powerful version control features when working with vector data.

We recently announced our intent to support Vector indexes in Dolt. If you're not familiar with vector databases, that post explains what they are, why they're useful, and what Dolt can add to your vector workflow.

But how exactly do we intend to accomplish this? How does one build a vector index out of Prolly Trees?

Back Up, What's a Prolly Tree?

We've gone into this in a lot more detail before, but to summarize the most important bits: A Prolly Tree is a Merkle Tree that stores an ordered list of elements, with the additional property that if two trees contain the same list, they have the exact same shape. We call this property history-independence. Most common tree implementations like B-Trees and Red-Black Trees don't have this property.

Prolly Tree implementations achieve history-independence via probabilistic hashing: the elements of the list are fed into a hash function, and the result of the hash function determines when boundaries are drawn between sibling tree nodes.

What's the Point of Prolly Trees?

Prolly Trees are incredibly useful because they have all the properties of Merkle Trees, but are also self-balancing, which makes them suitable for use in algorithms and databases. In particular, a data structure built out of Prolly Trees can have the following properties:

• Structural sharing and version control: store multiple versions of your data and effortless switch between them, reusing storage for the parts that are the same.
• Fast diff and merge: Comparing two branches should be fast when the differences between them are small, regardless of how much total data they contain. Merging changes together should be fast, and automatic when possible, just like git merges.
• Incremental pulling of updates: Downloading a new version of the dataset from upstream should only need to download the parts that actually changed, without needing a log.

We think that these properties are incredibly useful for a wide variety of applications. That's why we created Dolt as a SQL database that leverages the power of Prolly Trees. In Dolt, every table and index is implemented as a Prolly Tree.

Then we discovered we could build other things out of Prolly Trees too. Earlier this year, we began storing JSON documents on top of Prolly Trees, resulting in unparalleled speed for lots of standard JSON functions.

Naturally, we wanted to see what else we could build out of Prolly Trees. Could we use Prolly Trees to build a better Vector Index?

Vector Indexes, a Primer

A vector index is a precomputed data structure designed for optimizing an "approximate nearest neighbors search" for a multidimensional vector column. You can imagine vector indexes as a generalization of spatial indexes (which Dolt already supports) onto higher dimensions, but optimized specifically for a single type of search.

It's "approximate" because if the query is to find the N closest neighbors to some vector, it's okay if the result isn't exactly the N closest neighbors, we're allowed to miss some in the name of speed.

The accuracy of an index is called its "recall." Higher recall is better, but it's not the most important factor.

If Dolt already has Spatial indexes, why does it need Vector indexes?

In other words, could you just use a Spatial index as a Vector index?

Technically, you could. Spatial indexes work by placing every point on a space-filling curve, and then ordering the points in the index based on where they lie on the curve. Essentially, every value gets mapped onto a single dimension: a point on a line, and then that single dimension gets indexed. Close values in this single dimension roughly correspond to spatial locality. It would be easy enough to simulate a vector index on top of a spatial index, by using proximity along that curve as an approximation for distance.

Such an index would technically work. It would even be fast. But its recall would be pretty awful.

For example, look at the following example of a Z-order curve:

(Source: https://en.wikipedia.org/wiki/File:Z-curve45.svg)

In this image, 001111 is adjacent to 010000 on the curve, despite the two points being quite far apart. At the same time, 001111 is quite far from 110000 on the curve, despite the two points being spatially close.

More sophisticated space filling curves can address some of these issues, but only to a point. That's why, to the best of our knowledge, no real-world vector database uses this approach.

How are Vector Indexes typically implemented?

When discussing vector index design, there are typically three main algorithms with different tradeoffs.

Index Type 1: Full-table scan

This is just a brute force approach. No precomputation is done, and no extra storage is used. To find the closest neighbors of a vector, you simply compute the distance between it and every vector in the dataset, and put them all in a priority queue.

I wouldn’t even describe this as an index, but some sources do. Because this doesn't require any extra data structures, this is a plan that is always available if no explicit index has been defined on the vector column.

Surprisingly, this strategy actually has some advantages! It's the fastest to build (because you don't build anything), and for very small datasets it can still run in an acceptable amount of time. It also has perfect recall: you will always find the N closest neighbors of the target vector. As a result, a full table scan is actually used in real environments when recall is important, the data size is small, and memory is limited.

Index Type 2: Inverted File (IVF) Index

IVF is an indexing technique that works by organizing vectors into clusters. Computing the nearest neighbors of an input vector is done by first narrowing down which clusters can possibly contain the neighbors, and then and only calculating distances for the vectors in those clusters.

Typically, this is done by assigning a single "representative" vector to each cluster and doing a nearest neighbor search on the clusters themselves, then doing a second search on only the closest clusters. Implementations typically stop after a single level of clustering, but there's no reason why this can't be done recursively to create a hierarchical data structure.

The representative vector for each cluster is often the centroid (average) of every vector in the cluster. But this isn't required. The only requirement is that each cluster must contain exactly the vectors that are closer to that cluster's representative than any other cluster's representative. This means that the clusters partition the vector space in the manner of a Voronoi diagram.

These requirements are quite flexible and leave a lot of choices for the design. Some of these choices include:

1. How are the clusters determined?
2. How do we quantize our vectors?
3. Do we build a "multi-index" out of several indexes?

How are the clusters determined?

The most common approach is to use K-means clustering on the full dataset or some subset of the data. This produces a centroid for each cluster, which is used as the representative vector of that cluster. Usually, cluster boundaries aren't changed after the index is created. If newly added data has a different distribution than the data used to create the index, the speed and recall can suffer.

Whatever approach we take, it's very desirable that each bucket has approximately the same number of elements. This minimizes the worst-case performance, and also ensures that the density of the data is reflected in the density of the buckets.

How do we quantize our vectors?

Quantization is a broad term that means "mapping values from a large set onto values from a smaller set."

Quantization can reduce the size of an index, and even speed up operations, but often at the cost of recall. Separating the vectors into clusters is one kind of quantization. Two other common kinds of quantization include:

Reducing the precision of vectors

Even if the original data uses 64-bit floats, an index could use floats with much smaller precision without meaningfully affecting recall. Using less precise values likely won't speed up floating point operations, but it will reduce the space required to store the index.

Reducing the number of dimensions

Lots of algorithms that work well for a smaller number of dimensions can suffer unexpectedly as the number of dimensions increases. This principle is called the Curse of Dimensionality. Machine learning models may use vectors with hundreds of dimensions: how do we prevent the Curse of Dimensionality from becoming a problem?

Here's a nifty trick: what if we reduced the number of dimensions in the index? For example, our dataset uses 512 dimensions, but when building the index, we project each vector into only 32 dimensions. This can massively speed up the search, at the cost of some false positives. Once we have a list of top candidates, we re-run the search using the full 512 dimensions, but only on those candidates.

If we do this, we can speed up the search, but we're effectively ignoring most of the data in our vectors which could affect accuracy. But there's a way to counteract this loss of recall...

Do we build a "multi-index" out of several indexes?

If we reduced the number of dimensions of our index, we could still incorporate the dropped data by creating "multi-indexes" which combines multiple smaller indexes. A multi-index applies multiple different projections to each vector and then has a separate inverted index for each projection, each with their own set of clusters. The nearest neighbor search is performed on each index, and then the results are intersected.

Thus, a multi-index allows for all of the data in the vector to be used while still keeping the number of dimensions manageable.

Index Type 3: Hierarchical Navigable Small World (HNSW)

Hierarchical Navigable Small World indexes work by creating a graph where the vertices are the vectors, and the edges represent close neighbors. With a graph like this, a greedy graph traversal can be used to find the vectors closest to some query: start anywhere in the graph, visit its neighbors, and keep visiting whenever an edge brings you closer to the query.

This works, but would be slow for large datasets. To speed it up, the index stores graphs for multiple "layers", each of which stores only a fraction of the vectors from the previous layer. This is the "Hierarchical Nested" part of the name. With fewer vertices, edges in the higher layers cross larger distances and can traverse the search space more efficiently.

To find the nearest neighbors of some new vector, start at the top layer, the one with the fewest vertices, and walk the graph to find the vectors closest to the target. Once there are no longer any edges that bring you closer, drop down one layer and continue the process on the new larger graph.

This diagram from Pinecone's excellent online lesson series visualizes this process in a nice way:

(Source: https://www.pinecone.io/learn/series/faiss/hnsw/)

Inserting a new vector into the index involves computing the max level that includes the new vector, and then updating the graph in each level. The existing graph is used to compute the new vector's nearest neighbors, and those edges are added to the graph. If a vertex has too many edges now, delete the edges that are furthest away.

In practice, creating and updating HNSW indexes is slower than IVF indexes, and requires more storage space. However, queries are often faster.

And Beyond?

These aren't the only ways to make a vector index. This isn't a solved problem, and there's room for these techniques to be modified and combined.

Summary of existing algorithms

Here's a summary of the three algorithms described above. Each one has their own tradeoffs:

	Index creation time	Incremental update time	Query time	Storage needed
Full table scan	none	none	slow	none
IVF	fast	fast	mid	small
HNSW	slow	slow	fast	big

Typically:

• Full table scan is used for small data sets or when exact matches are required
• IVF is used when the index needs to fit in a small amount of memory
• HNSW is used when query time is the most important factor, and memory is not a concern.

All three types have their uses. Ideally, we'd like to implement all three types in Dolt. If we can build each of these indexes out of Prolly Trees, and make these versions history-independent, then it would open the door for vector databases that can be easily version controlled, compared across versions, forked and merged.

Building a Full Table Scan Index with Prolly Trees

Building a Full Table Scan Index is trivial, because there's nothing to build! Given that this see real-world use, we definitely plan on supporting it.

Building an Inverted File Index with Prolly Trees

The most important decision in building an IVF index is how to partition the vectors into clusters. Unfortunately, the most common method (K-means clustering) won't work for us, because it depends only on the vectors in the data set at the time the index is built, and the cluster boundaries can't be changed afterward. We would need some other way to partition the vector set.

One option would be to take the same probabilistic hashing that we use to split Prolly Tree nodes and use it to randomly select vectors to serve as the cluster centers. Whenever a new vector is added to the data set, we use this same hashing method to decide whether it results in a new cluster, and if so we check the vectors in neighboring clusters to see if any of them need to move.

This method means that most updates are nearly instant, while the small fraction of updates that create new clusters will be slower as we rebuild the modified clusters. The average runtime of this operation would still be fast, although the distribution function is a bit lopsided: mostly fast operations with occasional slow ones.

However, there's another subtler problem: building an index like this requires us to identify the clusters, then sort vectors into them. If we imagine the index as a tree, then we start by building the root, and end at the leaves. But that's not how Prolly Trees work. Prolly Trees, like other Merkle Trees, are always built from the leaves. Thus, it becomes very tricky to modify the index without loading it fully into memory.

This issue is not insurmountable, and we have ideas for how to overcome it.

Building a Hierarchical Navigable Small World Index with Prolly Trees

Although it is not immediately obvious, the process of building and updating a HNSW index can depend on insert order.

Consider a HNSW graph with a single layer, and a max degree of 3 for each vertex. We might have a graph that looks like this:

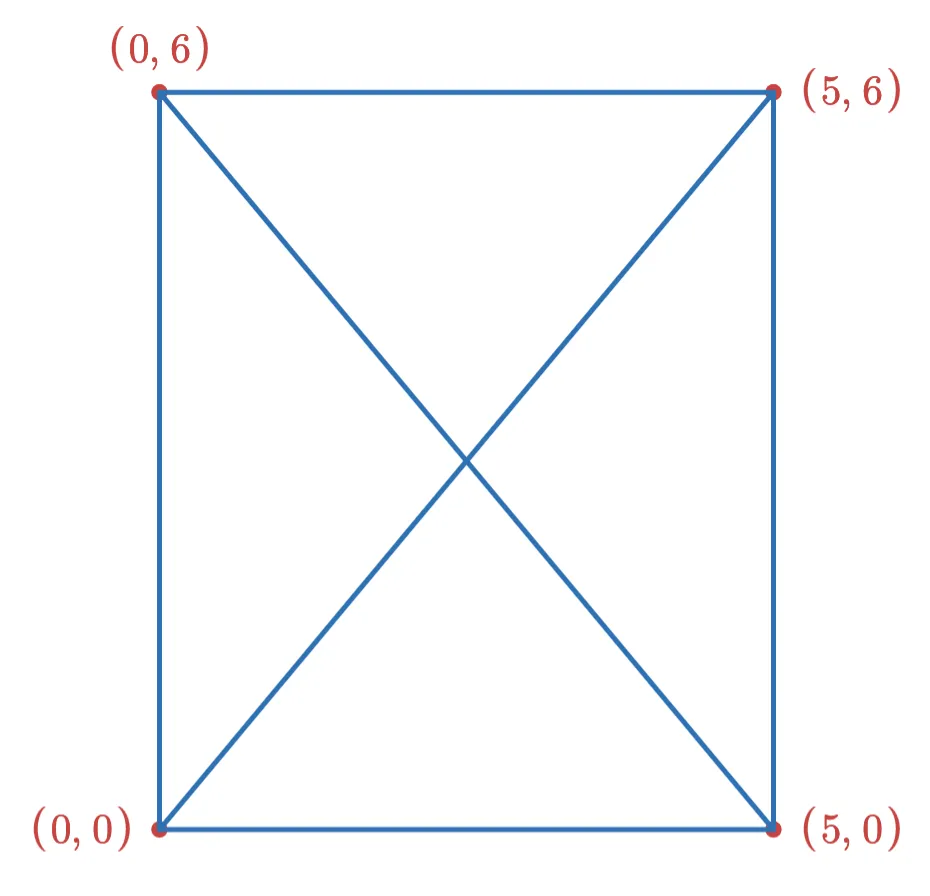
Now suppose we want to add the following two points to the index:

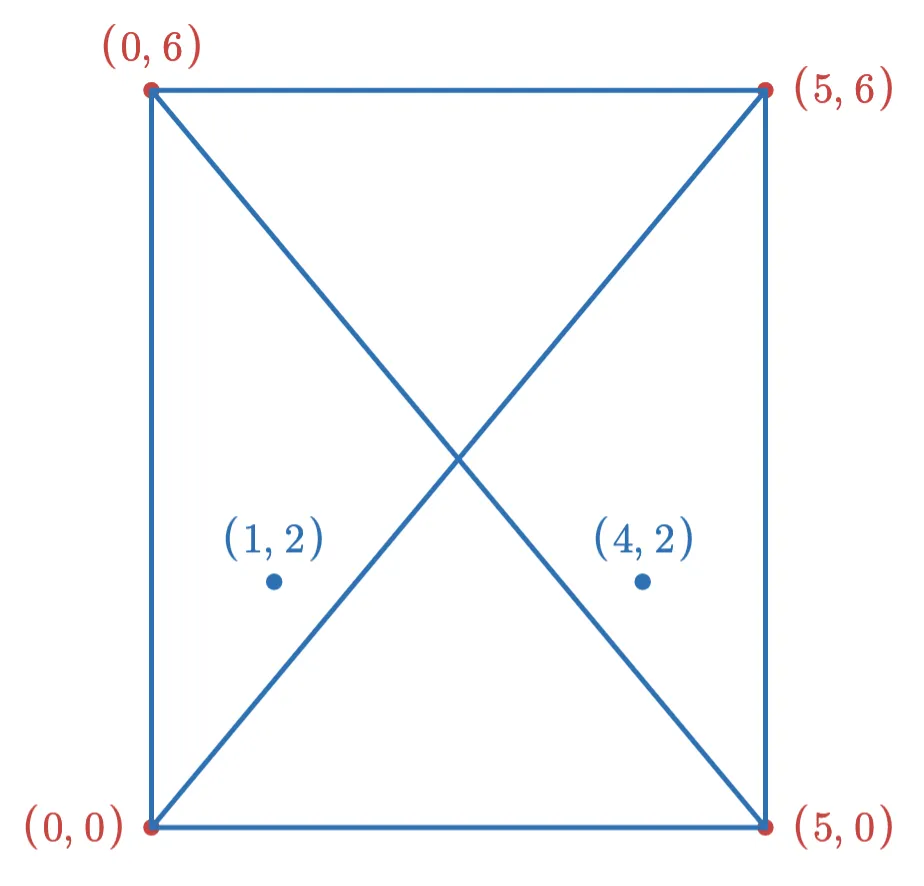
If we add the point (1,2) first, then after adding the new edges (and removing edges to keep the max degree at 3), the graph looks like this:

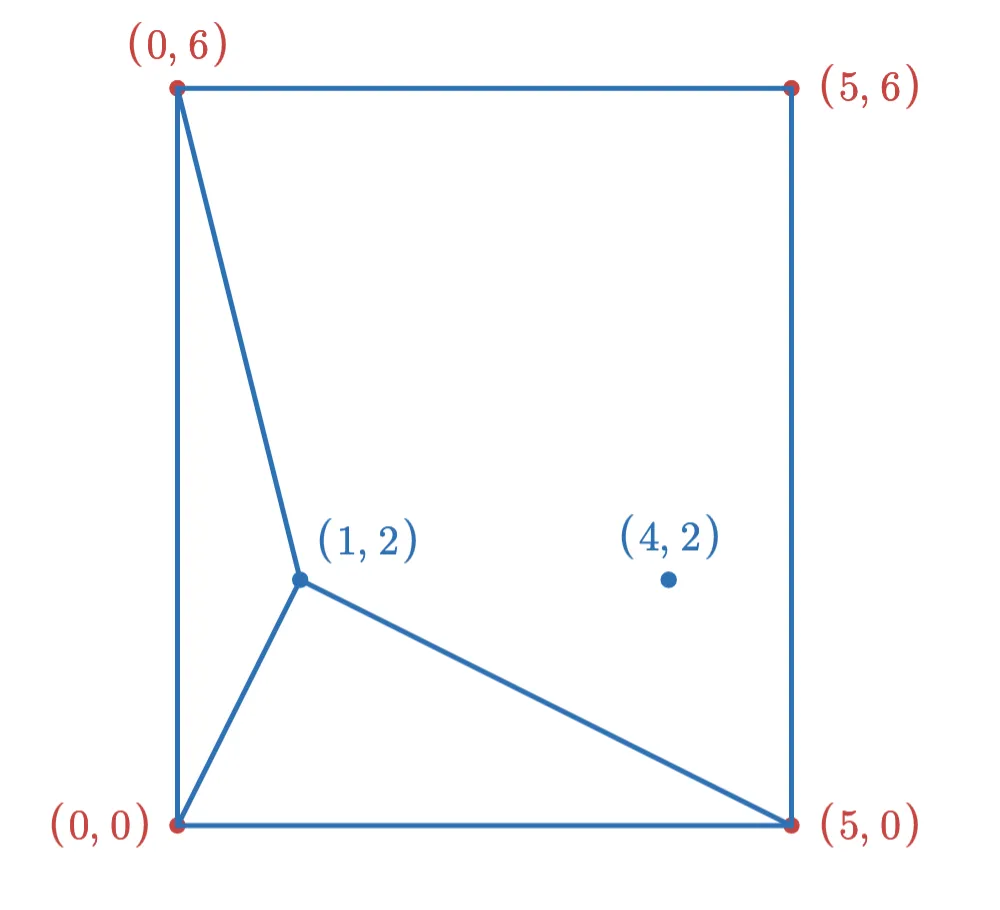
After adding the (4,3) point, the final graph looks like this:

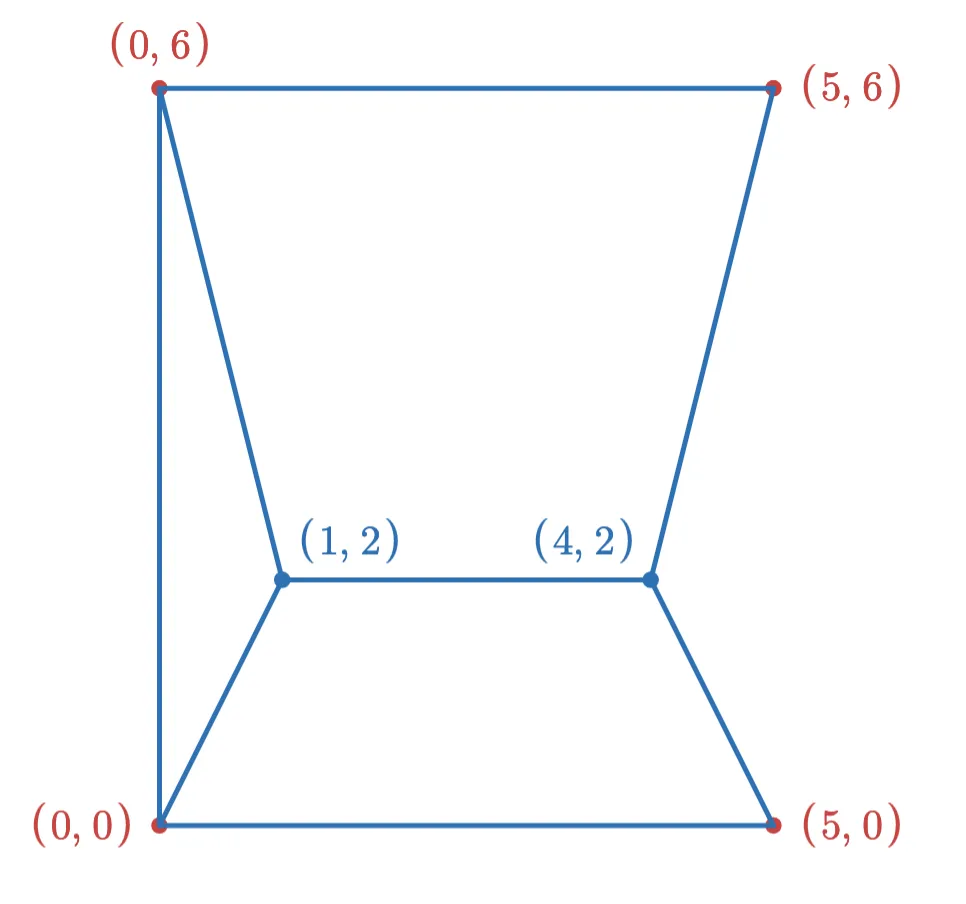
However, if we had added the points in the opposite order, the graph would have looked like this:

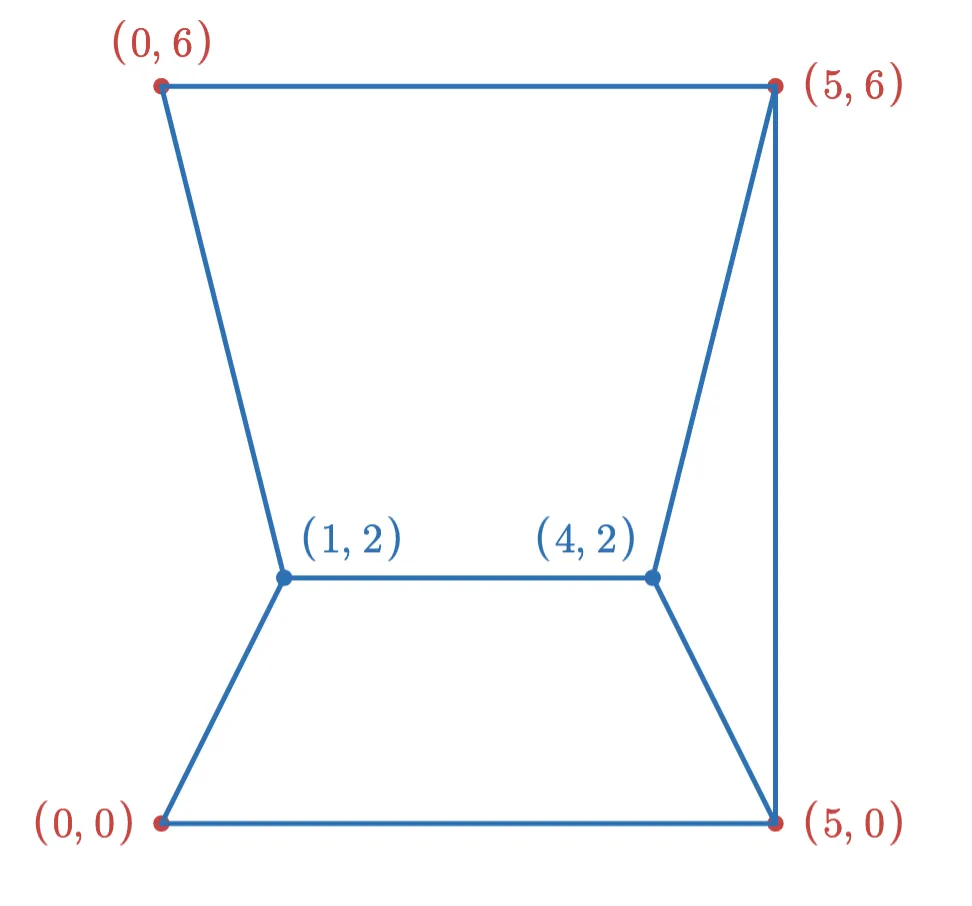
In order to make this not depend on insertion order, we would need to find some invariant that guarantees a given table of vectors always produces the same graph. Preserving this invariant during updates may result in more complicated logic and slower update times.

If we can solve that, the second big obstacle is figuring out how to use Prolly Trees to represent the graphs efficiently. Prolly Trees are Merkle Trees, which can't contain cycles. But the small world graphs contain many cycles. We will need to represent the graph some other way, such as a list of adjacency pairs. It's important that small changes to the table lead to only small changes in this representation, otherwise the cost of updates might drastically increase.

We have ideas for this too. We weren't able to find any prior research into building HNSW indexes with Prolly Trees, but we're optimistic that it can be done.

The Battle Plan

After considering the requirements, we believe that all three types of vector indexes have real-world uses, and all three can be implemented in Dolt in a way that leverages Dolt's version control capabilities. Between the two non-trivial indexes, we decided to start by trying to implement Inverted File indexes.

We think this is really exciting work. To the best of our knowledge, no existing database has branches and version control for vector data. If Dolt succeeds in implementing vector indexes using Prolly Trees, we would become the first.

We're thrilled to be going on this journey, and we're glad to have you with us. If you think this is as exciting as we do, feel free to join our Discord and drop us a line! We love hearing from people who think this is as cool as we do.