Dolt Storage: The Case For Dictionary Compression
Last week, I reviewed the storage system used to store bytes on disk for Dolt databases. As I mentioned at the time, it's not perfect, and we are considering changes to the format. I've been researching this primarily through the lense of space utilization, and there is room for improvement.
Today I'm going to layout some of the findings I've made over the last month, and that will lay the foundation for what our upcoming changes in the storage format.
Bytes Bytes Bytes
As discussed last week, the storage layer for Dolt is entirely based on byte buffers with 20 byte keys. We call these "Chunks" and given the content addressed keys, they are foundational to Dolt's Merkle DAG data model. Chunks are used for all data, not just the Prolly Tree data which makes up the database tables and indexes. The commit details for a single commit are stored in a single chunk, for example. Nevertheless, most of the Chunks are related to Prolly Trees, so lets review what a change to a Prolly Tree looks like in terms of Chunks.
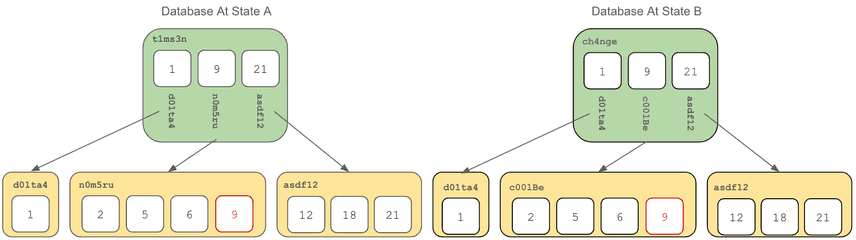
From our most recent review of Prolly Trees, the following picture should look familiar:
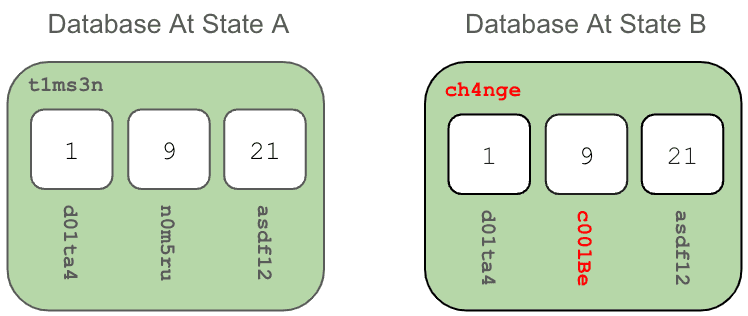
The yellow nodes are what you would consider your data. These include the rows of information that make up your database, and they can contain thousands of rows depending on your schema. To refresh your memory from the post where this picture came from, the red "9" in the middle leaf node is a primary key to a row, and a value in that row has changes. By doing this, the leafs content has changed, so you can see that the middle nodes address has changed from n0m5ru to c001Be, and by virtue of that address changing, the values in the green boxes have been updated, which changes their addresses from t1ms3n to ch4nge.
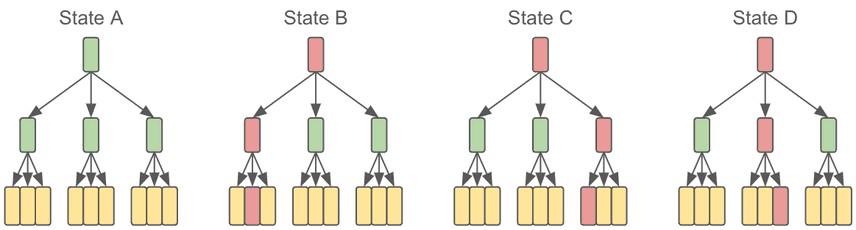
To further the point, let's zoom out a bit, and look at a series of changes to a larger tree. These are serial changes where each change builds from left to right.
To make it even more specific, if you have a data table which uses strings as keys, those keys will be sorted in the Prolly Tree. State A being your original unchanged state, then B,C, and D would come up with three commits to your data.
db1/main> show create table word_count;
+------------+------------------------------------------------------------------+
| Table | Create Table |
+------------+------------------------------------------------------------------+
| word_count | CREATE TABLE `word_count` ( |
| | `word` varchar(32) NOT NULL, |
| | `count` int, |
| | PRIMARY KEY (`word`) |
| | ) ENGINE=InnoDB DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_bin |
+------------+------------------------------------------------------------------+
db1/main> UPDATE word_count SET count = 42 where word = "git";
db1/main*> CALL DOLT_COMMIT("-am", "update git to 42"); // STATE B
db1/main> UPDATE word_count SET count = 51 where word = "takes";
db1/main*> CALL DOLT_COMMIT("-am", "update takes to 51"); // STATE C
db1/main> UPDATE word_count SET count = 23 where word = "mastery";
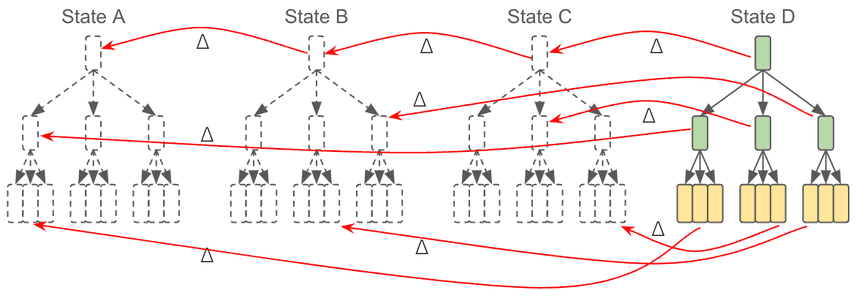
db1/main*> CALL DOLT_COMMIT("-am", "update mastery to 23"); // STATE DWith each update to your database's tables, the nodes colored red need to be updated. This is inherent in using a Merkle Tree to represent our database state. If you change anything at a leaf node, all layers above it must be updated as well. This is really important for how Dolt can track all history of your data. This results in a new problem though.
Going back to these two Prolly Tree Layer nodes, if we remember that there can be hundreds (or thousands!) of unchanged addresses in that data. Even though t1ms3n and ch4nge are 99% the same, the model I've described above mandates that an entirely new chunk is required.
This is the natural consequence of content addressed storage. So while we love all the virtues of Merkle Trees and DAGs, and we have to remember that it created new problems for us to address. Efficient use of disk space is definitely one of them.
What Git Does
Git uses Merkle Trees to represent source code content. Files themselves are called "blobs", and the intermediary layers are trees, which are effectively directories. Each blob and tree is content addressed, and Git has the same problem that is described above. When you change a single line of code, the file becomes a new blob with a new address, and every directory (tree) needs to be updated all the way up to the root tree node.
Git's storage system uses Delta Compression to minimize the amount of data it actually stores on disk. I'm talking about fully garbage collected Git repositories here. The idea seems straight forward: Preserve the current content, and store the reverse deltas of each changed object. Using the reverse deltas, you can take the current HEAD, and walk backwards in history applying the delta at each step on the walk to get to the content for any point in history.
Git does this remarkably well. Its funny to realize that when you execute the following command:
git diff HEAD~5..HEAD
It actually needs to calculate 5 reverse deltas before it can render the forward diff that you actually asked for.
Git also takes some shortcuts. Have you ever noticed that Git can't store binary files very well? That's because they punted on binary delta encoding. Tree objects internally are represented at text files, so they get to use simple text diffs there too.
Can Dolt Do That?
When I started looking into this problem, I was pretty sure that a similar reverse delta approach would be workable for Dolt. The main difference for Dolt is that all of our data is binary data. Writing a binary delta algorithm is definitely something someone else has done, right? With a little research, it became apparent that binary delta calculation was the first step of all modern compression algorithms.
Take a moment to consider what compression means in the general case. In order to compress anything, you need to find common patterns that repeat in your data stream. Using the highest frequency strings of bytes which match, you convert those into shortened words. So if you have the phrase "All work and no play" multiple times in your document, you can shorten that to a short identifier and encode that into your output stream. Then, when you decompress, you use start with that dictionary of terms, then expand the shortened version into the correct value when decoding.
That first step, finding the highest frequency strings of bytes, is effectively the same task as generating a diff of two binary objects. In fact, binary delta calculation sufficient for a delta encoding scheme would be the simplest and narrowest scope of what general compression has been doing very well for years. General compression has had a tremendous amount of research effort, while binary delta calculation is simply a very narrowly scoped but related problem.
Given that, I was curious how well gzip would work on the raw data of a real Dolt database. Using the real databases, I pulled all the history down for the databases below and ran dolt gc. This results in putting all Dolt data into one file, which we call a Table file. Table files were covered in detail last week in the Storage Review, and a subtle detail there is that we currently use Snappy compression on each individual Chunk in storage. With a few tweaks to the code, I disabled Snappy compression and generated a new file, which was significantly larger. This tells us that Snappy compression is already reducing our data footprint by a significant amount.
Taking that expanded (uncompressed and raw) version of the storage file, gzip can compress that file to significant amount smaller than Snappy on a per-Chunk bases.
| Repository | Raw Footprint (Mb) | Snappy Footprint (Mb) | Snappy % improvement | Gzip Footprint (Mb) | Gzip % improvement |
|---|---|---|---|---|---|
| Stocks | 1849 | 790 | 57% | 513 | 72% |
| SHAQ | 1219 | 500 | 59% | 305 | 75% |
| Investment Data | 36180 | 18024 | 50% | 9002 | 75% |
Knowing that general compression is pretty amazing, I knew that there would be no way to do better than the gzip value if we didn't leverage some application knowledge about the data.
We also have one additional requirement which is that we need to load Chunks in arbitrary order. Simply compressing the entire file wasn't an option because most compression algorithms don't support random access, and the ones that do have other downsides. Some expense was going to be required to allow us to randomly access chunks stored on disk.
These are our two primary goals now:
- Have total compression of the storage file be comparable to Gzip result of ~75%.
- Allow direct read access to each chunk. Putting the Index lookup time aside, the data retrieval from the data block must be constant time, and not load unnecessary information.
With this knowledge and goal in hand, I attempted to use the Go-Delta package to calculate deltas between chunks and come up with a way use Dolt history to delta encode chunks in the storage format. Unfortunately the Go-Delta package adds 156 bytes of overhead for every delta, so I ran into a wall pretty quickly. In the Stocks repository, for example, there are ~500K chunks, so if we delta encoded just 20% of them, that's an added 30Mb of space used just to encode the deltas themselves.
Delta Encoding for Dolt proved to be hard. There was a lot of complexity involved in tracking back multiple deltas, and the payoff was minimal. From a compression perspective, we went from compressing Chunks individually to considering them in pairs. Compression gets better if you have more data because the chance of repetitions is higher. So, back to the drawing board we went.
Dictionaries
There is a better way: zStd Custom Dictionaries. zStandard is a compression algorithm developed by Facebook, er. Meta, to help them store and transmit fewer bytes at scale. Right in the header of their docs, they say:
It also offers a special mode for small data, called dictionary compression.
Well that's intriguing. What magic is this?
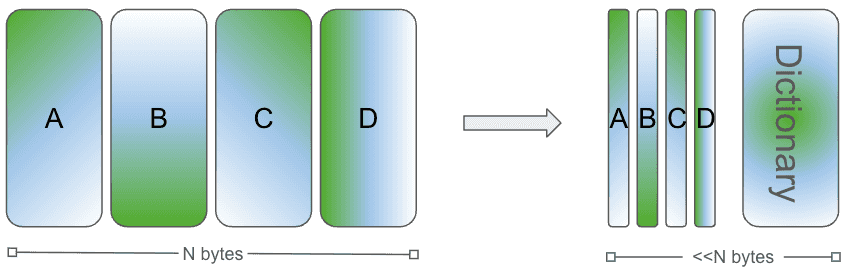
Custom Dictionaries allow you to train on a set of data, and produce an artifact which is a Dictionary that would work well to encode the provided training data. As mentioned above, general compression works by creating a group of common words that repeat in the data, then those words are referred to with short identifiers in the encoded data. Custom dictionaries give us the ability to keep the dictionary separate from the compressed bytes. We can effectively get the compression performance of compressing all similar chunks in one group, but maintain the ability to keep each Chunk as an individual data block that we can read off disk.
Given that Dolt has many Chunks which are very similar, we decided to test if we could reduce total space used by training the dictionary with related Chunks, then store the dictionary along with the compressed Chunks.
If we limit the Dictionary size to the average size of the chunks in question, then we end up with very small compressed objects. In some of our exploratory tests, we could reduce ten 4K Chunks down to a 4K dictionary with the Chunk objects taking up 20-200 bytes. In some specific groups of real data, we achieved as much as 90% compression. That's not possible over the entire dataset, but if we had enough pockets of highly related data, all those individual gains could help us break the gzip goal of 75% compression. And we'd still be able to have constant time disk reads.
It was a theory, anyway. We needed to run some tests.
Experiments
We had a lot of unknowns on what to do with this information. In order to assess our options we want considered three compression strategies:
- Use zStd as a direct replacement for Snappy. No dictionary.
- Use zStd with a global default dictionary to compress all Chunks.
- Use zStd with grouping of Chunks which are highly related with their own dictionary. Default dictionary for ungrouped Chunks.
In order to test those ideas, I had to take a side quest to implement a new storage format so that we could actually write these objects to disk in an efficient way, and have high confidence that this wasn't smoke and mirrors. Tune in next week for more on that. The other sanity check I added to our testing was to read out every Chunk from the archive and verify its contents matches its address. Thanks to Dolt's reliance on Content Based Addresses, we have a built in mechanism to ensure we don't break the Chunk datastore.
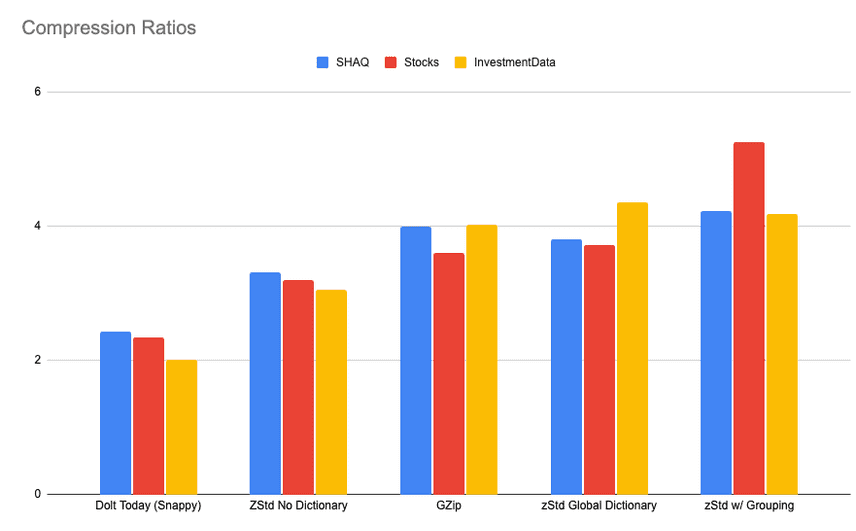
So, with all that out of the way, here are the results:
Gzip being the goal, Dictionary compression puts us ahead. The Default dictionary resulted in better than Gzip performance, while we continue to be able to load the Chunk in one disk read. While Compressing with additional group information, we were able to squeeze even more performance out of two of the repositories. The Investment Data history did not work well with my efforts to group similar chunks, as I was only able to group 2% Chunks, while in the SHAQ and Stocks databases, I was able to get effective grouping for ~30% of all Chunks, and it did measurably improve compression.
Included below are data tables as well. The take away is that it's possible to get much better use of our disk space with the adoption of zStandard compression. Dolt's disk use will be as mush as 50% lower when we complete the work to get it in your hands.
What Work Remains?
All of the experiments above were done with a CGO implementation of zStd. Here at Dolt we really pride ourselves on using Go as much as possible. There is a Go port of zStd which we are evaluating, but we do have some work to do to get to the performance numbers listed here.
Performance testing is also required to make sure that your database still performs well with the new storage format. There will probably be some things to improve and tweaks to the format before we can put this in your hands.
Finally, more effective grouping of chunks. I didn't go into detail on how that was done, but it's fair to say there is a lot of room for improvement. Using the Dolt commit history we can associate Chunks as similar by virtue of them both being part of a update of the Prolly Tree in the same commit. Our experiment does use the history for this purpose, but there are many edge cases which could be filled. I did do some brute force tests to try and find perfect matching of groups, but it was prohibitively expensive to run on any real database. Also worth noting, if you simply group Chunks by total length, the grouping effectiveness is nearly as good as what is shown here. It's worth calling out that our current strategy for finding groups worked very well on the Stocks repository, and terribly on the Investment Data database. We'll need to find ways to group better across the board. First released version may just use the global default dictionary. We'll keep you posted.
Thanks for reading. If you have any questions or want to test this experiment on your database, here is the branch. Jump on Discord!
Appendix
Any Amazonians in the house tonight?
Total Compression.
Using a base value of a table file where not compression was performed, this is how much we compressed our three test databases our three experiments: zStd, zStd with a Global Dictionary, and zStd with Grouping of related Chunks.
| Repository | No Compression (Mb) | zStd | %Compressed | w/ Dictionary | % | w/ Groups | % |
|---|---|---|---|---|---|---|---|
| Stocks | 1849 | 577 | 69% | 496 | 73% | 352 | 81% |
| SHAQ | 1219 | 368 | 70% | 320 | 74% | 288 | 76% |
| Investment Data | 36180 | 11852 | 67% | 8305 | 77% | 8643 | 76% |
Improvement on Snappy
| Repository | Snappy (Mb) | zStd no Dictionary | %Improved | w/ Default | %Improved | w/ Groups | %Improved |
|---|---|---|---|---|---|---|---|
| Stocks | 790 | 577 | 27% | 496 | 37% | 352 | 55% |
| SHAQ | 500 | 368 | 26% | 320 | 36% | 288 | 42% |
| Investment Data | 18024 | 11852 | 34% | 8305 | 54% | 8643 | 52% |
Improvement on Gzip
And finally to compare to taking the raw form of the data in it's entirety with gzip, which would not have been a viable option, but highlights that we are hitting close to total information density!
| Repository | Gzip (Mb) | zStd no Dictionary | %Compressed | w/ Default | % | w/ Groups | % |
|---|---|---|---|---|---|---|---|
| Stocks | 513 | 577 | -12% | 496 | 3% | 352 | 30% |
| SHAQ | 305 | 368 | -20% | 320 | -5% | 288 | 6% |
| Investment Data | 9002 | 11852 | -30% | 8305 | 7% | 8643 | 4% |