Efficient Diff on Prolly-Trees
Dolt is a SQL database with Git-like functionality, including branch, merge, diff, clone, push and pull. This is the third post in a series of blog posts that explore the underlying datastructures that are used to table storage and core algorithms in Dolt. In the first post of this series we discussed a content-addressed sorted indexed structure called a Prolly-tree, which forms the basis of table storage in Dolt. In the second post, we looked a little bit at the commit graph and some specifics of structural sharing in Dolt's table storage across revisions of a table. In this blog post, we're going to look at how Dolt implements diff across two versions of a table by taking advantage of the structural sharing exhibited by Prolly-trees.
Diffs of Table Data
Diffs between commits in a Dolt repository show the schema and data differences between all the tables in the database at the two commits. In this post, I'm only going to talk about the algorithm and tree walk that Dolt uses to generate the data diff for a single table. How Dolt handles schema changes is a topic for another day.
Dolt's data diff for a single table calculates every row that changed,
was deleted or was added between the two Prolly-trees that store the
table data. For example, in our
stock-tickers
repository, diffing the symbols table between two recent commits
shows:
$ dolt diff otnhanvp3f1hff91tqptdm3gotevdgno 3oktb67bs4iceap5b19q6o5fb52hsfv8 symbols
diff --dolt a/symbols b/symbols
--- a/symbols @ 0k1tfpao4nogimae66r90urfpvr6jfvm
+++ b/symbols @ 8l6scmsnkme57h0ohj7inlhs014ocmur
+-----+----------+---------+---------------------------------------------------+----------+-------------------+-------------------------------+
| | exchange | symbol | name | ipo_year | sector | industry |
+-----+----------+---------+---------------------------------------------------+----------+-------------------+-------------------------------+
| < | nasdaq | AIQ | Global X Future Analytics Tech ETF | <NULL> | <NULL> | <NULL> |
| > | nasdaq | AIQ | Global X Artificial Intelligence & Technology ETF | <NULL> | <NULL> | <NULL> |
| < | nasdaq | BNR | Burning Rock Biotech Limited | <NULL> | <NULL> | <NULL> |
| > | nasdaq | BNR | Burning Rock Biotech Limited | 2020 | <NULL> | <NULL> |
| < | nasdaq | GBIO | Generation Bio Co. | <NULL> | <NULL> | <NULL> |
| > | nasdaq | GBIO | Generation Bio Co. | 2020 | <NULL> | <NULL> |
| < | nasdaq | HOOK | HOOKIPA Pharma Inc. | 2019 | Health Care | Major Pharmaceuticals |
| > | nasdaq | HOOK | HOOKIPA Pharma Inc. | 1995 | Health Care | Major Pharmaceuticals |
| < | nasdaq | LAND | Gladstone Land Corporation | 1993 | Consumer Services | Real Estate Investment Trusts |
| > | nasdaq | LAND | Gladstone Land Corporation | 2013 | Consumer Services | Real Estate Investment Trusts |
| < | nasdaq | NOVS | Novus Capital Corporation | <NULL> | <NULL> | <NULL> |
| > | nasdaq | NOVS | Novus Capital Corporation | 2020 | <NULL> | <NULL> |
| < | nasdaq | NOVSW | Novus Capital Corporation | <NULL> | <NULL> | <NULL> |
| > | nasdaq | NOVSW | Novus Capital Corporation | 2020 | <NULL> | <NULL> |
| < | nasdaq | PCVX | Vaxcyte, Inc. | <NULL> | <NULL> | <NULL> |
| > | nasdaq | PCVX | Vaxcyte, Inc. | 2020 | <NULL> | <NULL> |
| < | nasdaq | RNA | Avidity Biosciences, Inc. | <NULL> | <NULL> | <NULL> |
| > | nasdaq | RNA | Avidity Biosciences, Inc. | 2020 | <NULL> | <NULL> |
| + | nyse | AZEK | The AZEK Company Inc. | 2020 | <NULL> | <NULL> |
| + | nyse | IPOC | Social Capital Hedosophia Holdings Corp. III | 2020 | <NULL> | <NULL> |
| + | nyse | IPOC.WS | Social Capital Hedosophia Holdings Corp. III | <NULL> | <NULL> | <NULL> |
| - | nyse | KEM | Kemet Corporation | <NULL> | Capital Goods | Electrical Products |
| + | nyse | VTOL | Bristow Group, Inc. | <NULL> | <NULL> | <NULL> |
+-----+----------+---------+---------------------------------------------------+----------+-------------------+-------------------------------+A <,> pair means the row was modified—its previous value is
as in the < row and its new value is as in the > row. A + means
the row was added and a - means the row was deleted. Rows are
identified by their primary keys, which in this case is tuple of
(exchange, symbol).
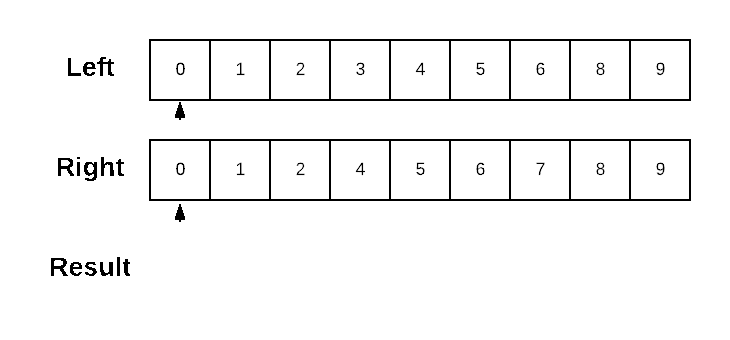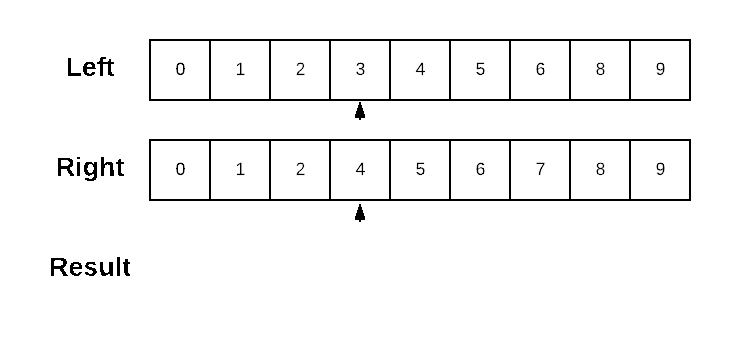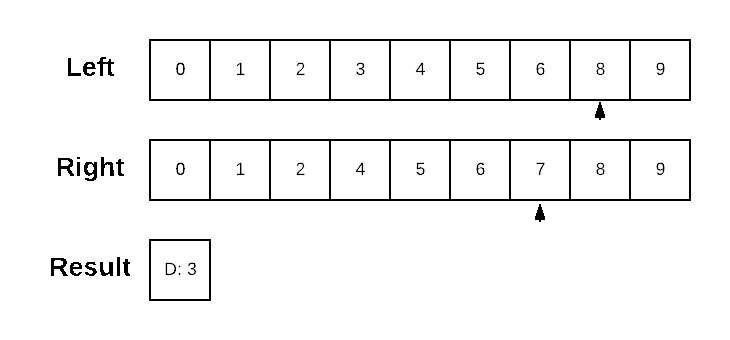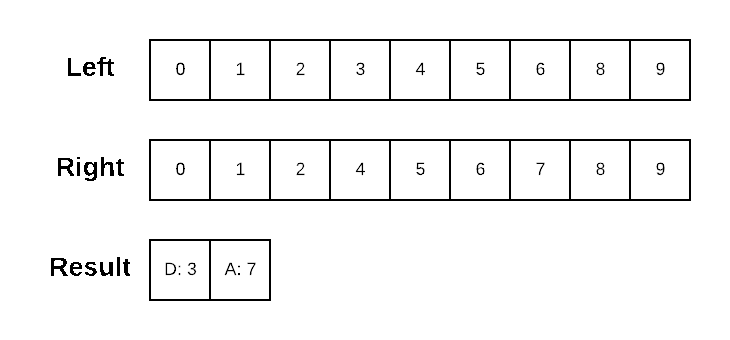
Dolt generates data diffs in primary-key order. The underlying algorithm is an in-order traversal of the two sorted structures, where anytime the values differ the lesser value is emitted as a difference and the position in the other structure stays the same. Let's quickly recap a simple sorted-list diff for review.
Left-to-Right Diff on Sorted Data
Because table data in Dolt is stored in a Prolly-tree, Dolt's data
diff is conceptually a function that takes two Prolly-tree values and
returns a list of differences between them. We can model the result as
a list of Difference values where each difference is one of three
types:
-
Remove an entry from the Prolly-tree. A key exists in
Leftand doesn't exist inRight. -
Add an entry to the Prolly-tree. A key exists in
Rightthat doesn't exist inLeft. -
Modify an entry in the Prolly-tree. A key exists in
LeftandRight, but it's value is different between the two trees.
We can implement a left-to-right Diff on a sorted structure by walking the values from each list in sorted order. When the current values aren't equal, we emit the lesser valued entry as a difference and advance our position in the list with the lesser valued entry.
An implementation in Go looks like this:
// A representation of the values in the leaves of the Prolly-tree.
type Value interface {
Less(Value) bool
}
// A Cursor allowing for in-order traversal of the values in the
// Prolly-tree.
type Cursor interface {
Done() bool
Current() Value
Next()
}
type Edit int
const (
Add Edit = iota
Delete
)
// A single changed value in a `Diff` of a Prolly-tree.
type Difference struct {
Op Edit
Value Value
}
// Returns all |Difference|s to convert |left| to |right|.
func Diff(left, right Cursor) []Difference {
var res []Difference
for !left.Done() && !right.Done() {
lv, rv := left.Current(), right.Current()
if lv.Less(rv) {
res = append(res, Difference{Op: Delete, Value: lv})
left.Next()
} else if rv.Less(lv) {
res = append(res, Difference{Op: Add, Value: rv})
right.Next()
} else {
// They are equal; no changes.
left.Next()
right.Next()
}
}
// Everything remaining in |left| was deleted.
for !left.Done() {
res = append(res, Difference{Op: Delete, Value: left.Current()})
left.Next()
}
// Everything remaining in |right| was added.
for !right.Done() {
res = append(res, Difference{Op: Add, Value: right.Current()})
right.Next()
}
return res
}An example run on two simple sorted lists might look like:
I've chosen to present the algorithm here on a sorted list for the
sake of simplicity. It's easy to extend to a Map when visiting the
keys in sorted order. It's also easy to convert the above code to
stream the Difference values to a result channel or a callback and
to allow for cancellation.
Efficient Diff With A Prolly-Tree
While the algorithm is correct, it is not particularly efficient. It will look at all values in both lists, even when they are exactly or mostly the same. The Prolly-tree and its structural sharing properties mean that we can do better. In order to do so, we need to change the behavior of the loop when the two cursors are pointing to equal values. We will change it to skip over identical portions of the Prolly-tree and jump to the the portion of the tree with the next difference.
But first, we need to expose some details from our Cursor interface.
We need to make Cursors expose content-addresses for the chunks in
the Prolly-tree so that identical portions of the tree can be skipped
over. Let's extend the interface a little bit:
// A content-address of a Chunk, for example, in a Prolly-tree.
type ChunkAddress [20]byte
type Cursor interface {
Done() bool
Current() Value
Next()
// Returns the content-addresses of the chunks on the path through the
// Prolly-tree to the current value, starting at the root of the tree.
Path() []ChunkAddress
// Advances the cursor at the specified height of the tree to the next entry.
// NextAtLevel(0) is equivalent to Next(). NextAtLevel(1) advances the cursor
// past the current entry on the first internal level of the tree---the one
// directly above the leaves. After advancing the cursor at an internal level,
// if the cursor is not `Done()`, the cursor points to the left-most entry
// accessible from the newly selected internal entry.
NextAtLevel(int)
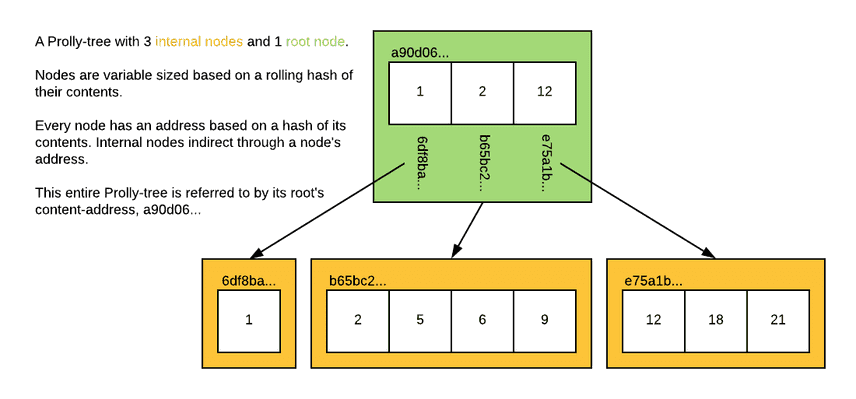
}On this example Prolly-tree:
when the Cursor is pointing at the value 5, then:
Path()is["a90d06...", "b65bc2..."]- After
NextAtLevel(0), the cursor would point at6andPath()would be unchanged. - After
NextAtLevel(1), the cursor would point at12andPath()is["a90d06...", "e75a1b..."]. - After
NextAtLevel(2), the cursor would haveDone() == true.
Exposing the current path from the root of the tree to the leaf entry
we are on will allow our Diff implementation to see structural
sharing between the two values. Adding NextAtLevel allows our Diff
implementation to efficiently skip over portions of the tree that are
shared between left and right.
To implement skipping when we have structural sharing, we use a short
helper function, FastForwardUntilUnequal. It takes two cursors and
advances them until either one of them is Done or ones value is less
than the other's:
// Advances |left| and |right| until one of them is Done or they are no longer
// equal.
// Postcondition:
// left.Done() || right.Done() ||
// left.Current().Less(right.Current()) ||
// right.Current().Less(left.Current())
func FastForwardUntilUnequal(left, right Cursor) {
for !left.Done() && !right.Done() {
lv, rv := left.Current(), right.Current()
if lv.Less(rv) || rv.Less(lv) {
return
}
level := GreatestMatchingLevelForPaths(left.Path(), right.Path())
left.NextAtLevel(level+1)
right.NextAtLevel(level+1)
}
}
// Returns the highest level in the tree at which the provided paths match.
// Returns -1 if there is no chunk address that matches, 0 if only the last
// chunk address in each path matches, etc.
func GreatestMatchingLevelForPaths(left, right []ChunkAddress) int {
level := -1
// Starting at the end of the two paths, compare the hashes in each
// path until they are not equal.
for li, ri := len(left)-1, len(right)-1; li >= 0 && ri >= 0; li, ri, level = li-1, ri-1, level+1 {
if left[li] != right[ri] {
break
}
}
return level
}And now our Diff implementation just calls out to
FastForwardUntilUnequal in the else clause, instead of calling
Next directly on both Cursors:
// Returns all |Difference|s to convert |left| to |right|.
func Diff(left, right Cursor) []Difference {
var res []Difference
for !left.Done() && !right.Done() {
lv, rv := left.Current(), right.Current()
if lv.Less(rv) {
res = append(res, Difference{Op: Delete, Value: lv})
left.Next()
} else if rv.Less(lv) {
res = append(res, Difference{Op: Add, Value: rv})
right.Next()
} else {
// They are equal; no changes.
FastForwardUntilUnequal(left, right)
}
}
// Everything remaining in |left| was deleted.
for !left.Done() {
res = append(res, Difference{Op: Delete, Value: left.Current()})
left.Next()
}
// Everything remaining in |right| was added.
for !right.Done() {
res = append(res, Difference{Op: Add, Value: right.Current()})
right.Next()
}
return res
}The new Diff implementation skips over portions of the tree that are
identical between the two values based on their chunk content
addresses. In practice, what happens is that Diff starts at the left
side of both trees. If there is no difference there, it skips at the
highest internal node in the tree that matches until it finds the
different internal entry in the parent node. Then it will skip
internal entries at that level until it finds the differing entry. It
will walk down the tree until it's at level 0, skip the entries at
level 0 that match and then emit the differences. Then it will start
skipping matching entries at level 0, until it synchronizes and starts
skipping entries at level 1, and then level 2, etc.
Here's a simple example of the walk on a 4 level tree. The compared
Prolly-trees have a branching factor of 2 and there is a single
different leaf cell, the beige leaf cell, between the two trees. The
Last Level indicator shows what parameter was passed to
NextAtLevel() for the cursors.
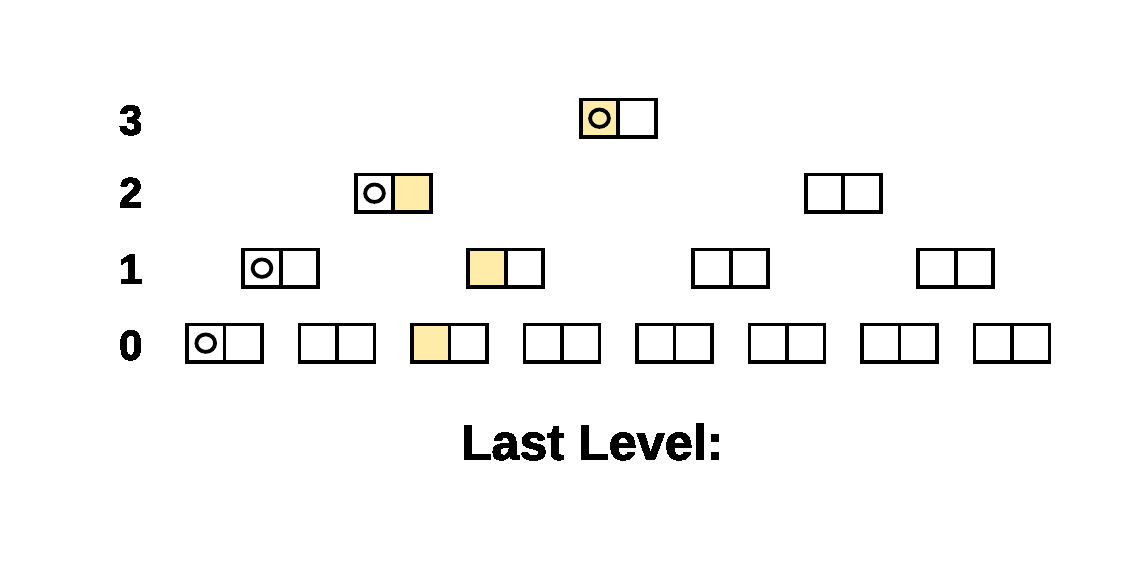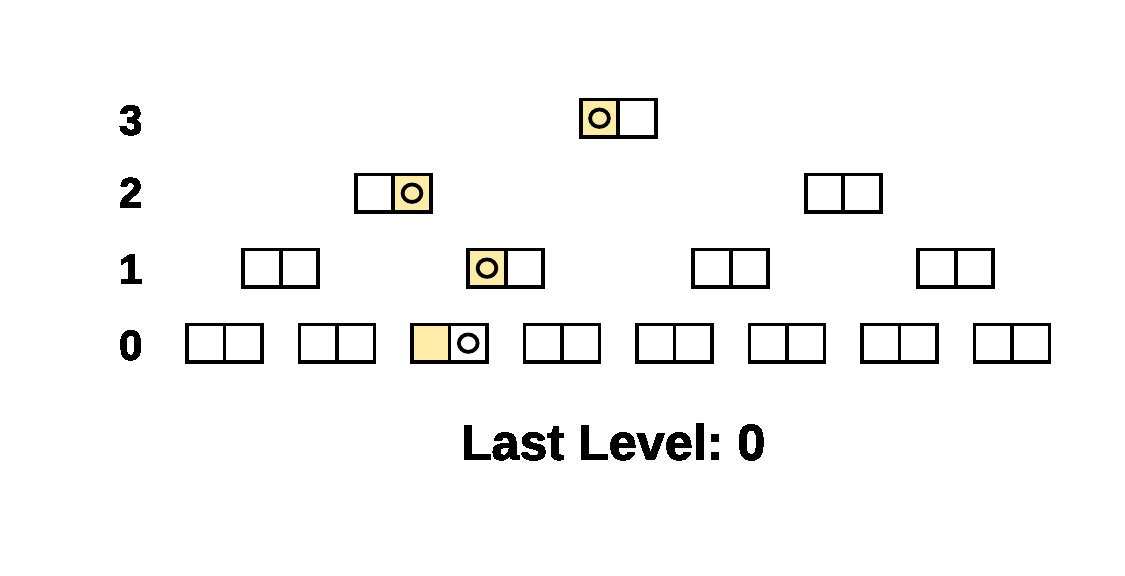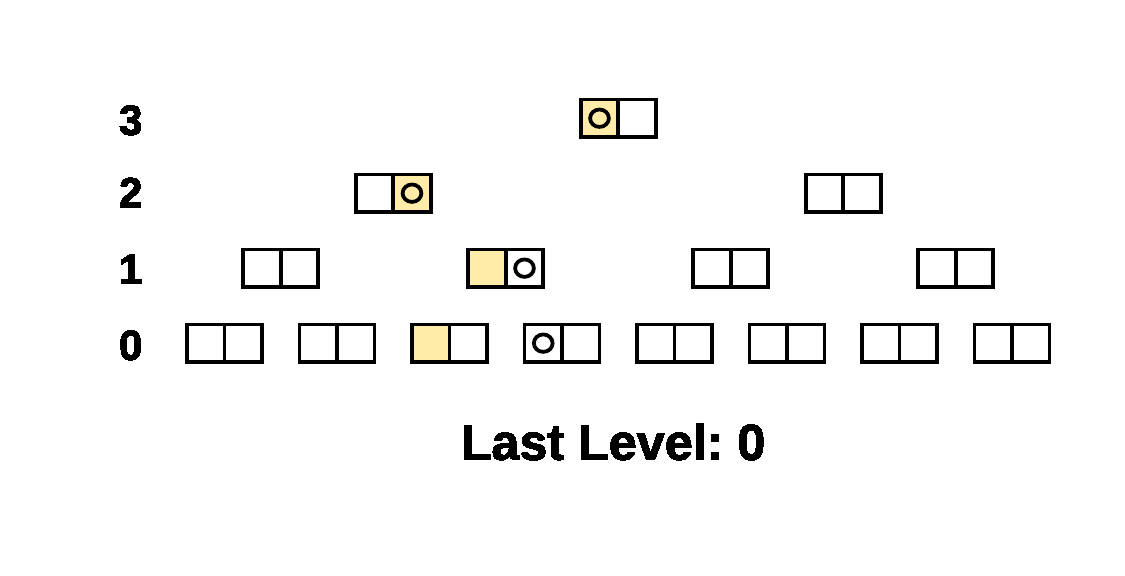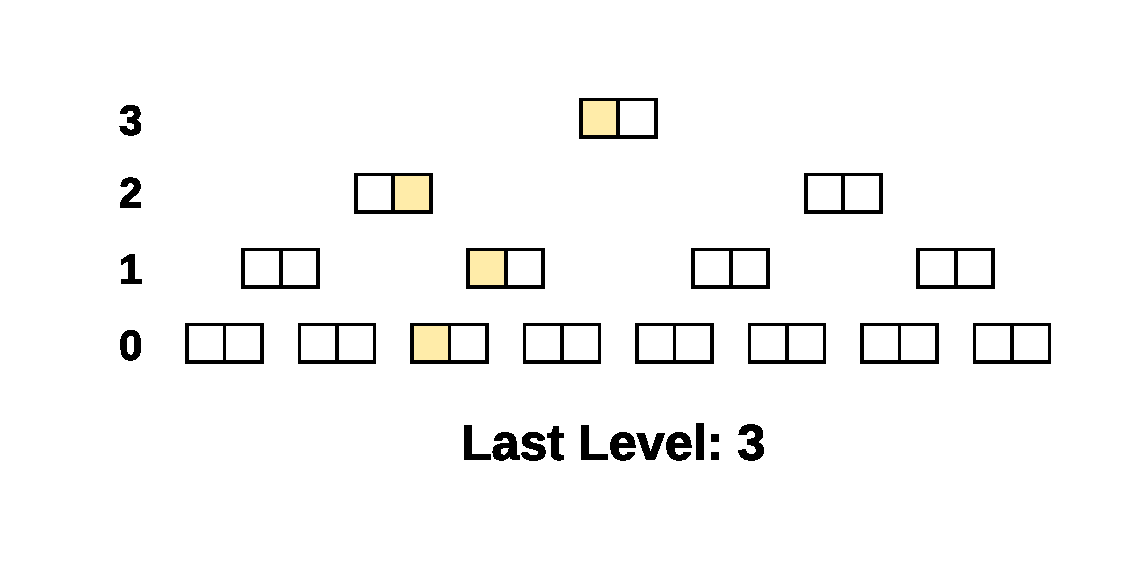
As you can see, when there is structural sharing, large subtrees of the tree can be skipped at once.
Conclusion
We looked at how Dolt implements diff for table data. By exploiting structural sharing in the Prolly-tree representation of two table values, Dolt's diff implementation can quickly find the portions of the tree where there are actually differences. Efficient diffs form the basis of DoltHub's cell history inspection, the dolt_diff system table and dolt's merge functionality.