In this blog post I want to give an introduction to some core concepts used to implement fast querying of databases. These techniques were implemented in Dolt and produced significant performance improvements.

Database internals

The B-Tree is a core data structure used throughout many databases. They provide lookups in log N time, can be traversed in order, and can be used to store tables, and indexes. A frequent operation in database development is selecting all rows that match a specific criteria. In SQL this looks like:

SELECT *
FROM table
WHERE <some criteria>

A naive approach to implementing this would do a full table scan, which walks the entire B-Tree in order and checks to see if any node matches the criteria. If the criteria being used to filter the results is indexed by the primary key or a secondary index then filtering can be optimized dramatically.

The Filtering Expression

The extent to which a database provides filtering functionality may very dramatically between databases. Many NoSQL stores only provide key lookups, some provide range queries on keys, others way provide secondary index lookups with or without ranges, and SQL provides extremely expressive filtering via the "where" clause. Regardless of the capabilities of your database, filtering on an indexed field can lead can lead to a drastically smaller number of rows being examined. To do this we need to build the set of keys which match the filtering expression.

Key Sets

A table with a primary key of id and the filtering clause id == 1 would be implemented with a simple B-Tree lookup. Similarly id == 1 or id == 2 or id == 3 would be implemented by lookups on the set of keys {1,2,3}.

A table with a primary key of date and the filtering clause date >= 2020-1-1 would be implemented with a lookup of the date 2020-1-1, and iterating forward until we've exhausted all keys. We can say that the keys are in the open interval [2020-1-1,∞). Depending on your the data in your table this may eliminate a large portion of rows, or it may be equivalent to a full table scan. If the filtering clause was date < 2020-2-1 instead, we would say that the keys are in the interval (-∞, 2020-2-1) and we would implement this with a lookup on the date 2020-2-1 and iterate backwards until all keys were exhausted (Note: In this case the value 2020-2-1 is not included in our interval, so it should be iterated past before the first value is returned by the iterator).

All of our possible key sets can be built by some composition of sets of discreet values as we saw in our first example and intervals as we saw in our second example. Two special which we will also talk about are the set containing no values, the empty set {} or Ø, and the set containing all possible keys, the universal set (-∞,∞) or 𝑼.

If there is no filtering clause, or all filtering is done on non-indexed fields, then no value of our keys will be eliminated. In this case our set of keys is the universal set 𝑼.

Building the Key Set for Complex Filtering

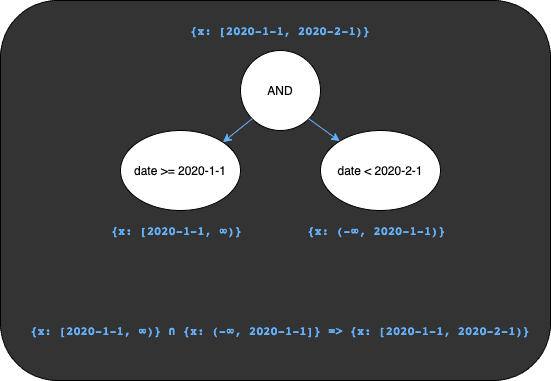
Going back to the date-indexed table from our previous example, the filtering clause date >= 2020-1-1 AND date < 2020-2-1 has a very clear intent to get all the values in January of 2020. The first expression yields the set of keys in the interval [2020-1-1, ∞) and the second expression will be the set of keys in the interval (-∞, 2020-1-1). The AND operator indicates we want only the values that are in both sets, also known as the intersection of these two sets, which is the interval [2020-1-1,2020-2-1). We can visualize this using the binary expression tree below

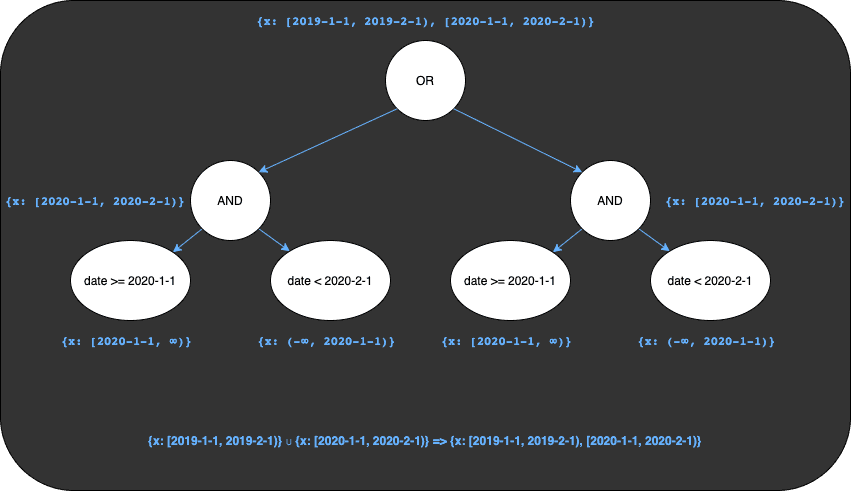
If I wanted to filter my results to the set of rows in January of 2019 and January of 2020 I would use the filtering expression (date >= 2019-1-1 AND date < 2019-2-1) OR (date >= 2020-1-1 AND date < 2019-2-1). Each of the expressions grouped by parens is in the same format as what we saw above and yield the sets [2019-1-1, 2019-2-1) and [2020-1-1, 2020-2-1) respectively. When we process the OR operator that joins these two groups we take all keys that are in either of the sets, also known as the union of the sets.

These rules can be used to build arbitrarily complex filtering logic which we will use to limit the amount of data we look at as we iterate through our table. For example:

(subsystem = "billing" and date >= 2020-1-1 and and date < 2020-2-1) OR date = 2020-3-1

Uses the same logic we already saw. The three filtering criteria inside the of parens yields the set of keys 𝑼, [2020-1-1,∞), (-∞,2020-2-1) (𝑼 the universal set is the result of filtering on the un-indexed field "subsystem"). The three criteria are joined with AND operators which means we need to intersect the three sets. As the intersection between any set S and 𝑼 is just S itself, the resulting intersection is simply the interval [2020-1-1,2020-2-1). This would then be unioned with {2020-3-1}, resulting in the set of keys where the date is in the interval [2020-1-1,2020-2-1) or is in the set {2020-3-1}. This logic is summed up as:

{x:𝑼} ∩ {x: [2020-1-1,∞)} ∩ {x:(-∞,2020-2-1)} ∪ {x:2020-3-1} => {x: [2020-1-1,2020-2-1), 2020-3-1}

Key Set Based Iteration

Any possible key set can be expressed as a set of discreet values, and a list of intervals. Each of these needs its own iterator to retrieve values. As mentioned previously the iterator for the set of discreet values would do a lookup for each value in the set. Interval iterators start at either the beginning or the end and iterate through keys while the current key falls within the interval.

An important note is that there can be no overlap in the key sets, otherwise duplicate rows may be retrieved. In most of the cases I can think of this is undesirable. As an example, when taking the union of {x: (-10,0]} and {x: [0,10]} if your resulting set is {x: (-10,0], [0,10)} each of your interval iterators will return the row with key 0. The correct union would be {x: (-10,10)}. Even though the sets are equivalent mathematically, the iterators that would result from their creation would produce different results. Similarly {x: 5} ∪ {x: [0,10]} must be {x: [0,10]} and not {x: [0,10], 5} or else the row with key 5 (If it exists) would be returned by the discreet set iterator and the interval iterator.

Optimizing History Table Performance

Dolt is git for data. It uses a commit graph to model the history of the database over time. At every commit in the graph there are database tables implemented using a variation of a B-Tree. Dolt implements a history system table for every user table in the database. In querying the history table, every commit in the commit graph is iterated over, and the query is run on the table for each one. The initial implementation performed a naive table scan for every one of those commits. When putting together visualizations of NOAA temperature data it would take about 90 minutes to run the query:

SELECT station, commit_date, max
FROM dolt_history_air_temp
WHERE station = '70261026411' AND commit_date >= '1950-01-01 00:00:00' AND commit_date <= '2019-12-31 23:59:59'

The "air_temp" table is indexed on the "station" field. As we covered previously this where clause should limit the keys checked to the set {x: "70261026411} ∩ {x:𝑼} ∩ {x:𝑼} => {x: "70261026411"} which should just be a single row lookup on each state of the table in the commit graph. This change brought this query's execution time down to from 90 minutes using the naive approach to 15 seconds.

Give it a Try

The NOAA dataset has 120 years worth of history, and is the perfect dataset to demo the power of the history table. You can also check out the blog covering how the data was modeled and how it can be accessed.